Welcome to

Mathematics Laboratory

Mathematics Laboratory (ML for short) is a collection of tools for communicating and getting to understand mathematical concepts, relations, algorithms etc. The idea is to make math easier to "get into" and understand by visualization and interactivity, that can bring both figures and formulas to life.

In our own courses, we have used ML as follows: matlab/ML is used in class/lectures as an integrated tool for presenting new material, and later the students use the same tools in computer lab sessions and at home for further analysis and a full and confirmed understanding of the new material.

Based on matlab

Physically, ML consists of a collection of matlab files (of .m and .fig type), that you can easily download from this page and then run from within the matlab program. That is, ML requires matlab, and you start the ML tools directly from the matlab >> prompt.

An example

For a first example, you may want to download the files BISECT.fig and BISECTAdm.m, the purpose of which is to present the Bisection algorithm for solving equations of the form f(x) = 0.

To open this demonstration/lab tool, type open 'BISECT.fig' at the matlab prompt. A new window should pop up, with the graph y = f(x) of a sample function f(x), and a number of buttons and text fields as follows:

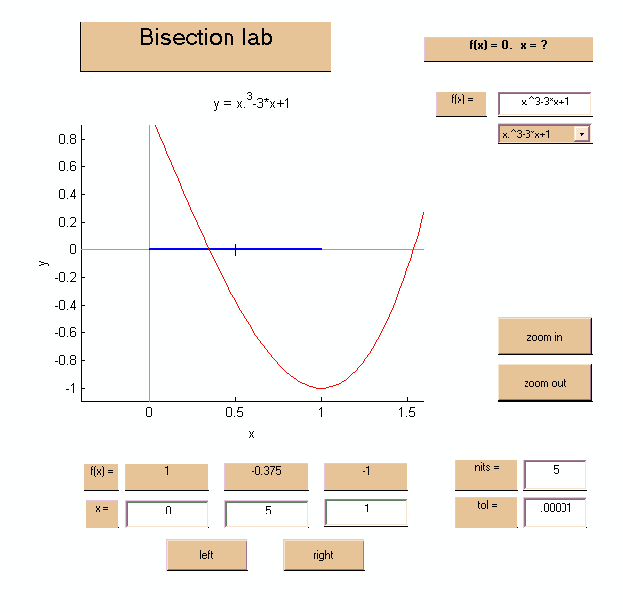
The idea is now for the user to select the subinterval hosting the zero of the given function, by pressing one of the buttons left of right, and then to repeat.

The idea is to give the students a more or less instant understanding of the algorithm this way, through a demonstration in a lecture.

Further, as the remaining interval, after a number of steps, gets too small to see easily, one is naturally led to rather use the corresponding f(x)-values as a basis for which sub-interval to choose, and then seek to write down the algorithm in terms of a logical "flow chart".

Based on the visualization of the Bisection algorithm offered by this "lab" one may also discuss

Implementation

We present the Bisection algorithm very early to our students, not so much because of its qualities as a solver, but rather because of its conceptual simplicity, and because implementing this method, which the students are set to do, involves most of the basic programming "elements" (an iteration loop, conditional statements, interesting logical considerations etc). That is, in our courses the students first meet this method in class, then get the chance to experiment on their own using the same tool in a lab session, and then to make their own implementation of the method from a code shell. For an example of how we have used these tools in a first math course for engineering students, see www.math.chalmers.se/cm/education/courses/0304/intro/.

Other solvers

Similar tools exist in the form of a FixedPointLab for the fixed point iteration algorithm, for equations of the type x = g(x), and a NewtonLab for Newtons method.

As an introduction to general equation solvers of this form, just to present the very idea of an iterative solution process, we have sometimes used the ZoomSolveLab where the equation f(x) = 0 is solved simply by succesive graphing and zooming. The limitation of this method, of course, is the difficulty to visualize the graph y = f(x) in higher dimension, that is, to generalize to systems of equations.

Shipping

The latter "labs" have been "packed" into an archive and then "zipped" for easy shipping in just one package. However, this means that you have to "unzip" and "extract" the individual files at arrival.

Help

The FixedPoint and Newton labs above (and several others to be presented below), come with a html help file that you start from within the lab to get tips on how the lab may be used and suggested problems.

All labs are opened from the matlab prompt with the command open 'labname.fig', where labname is the name of the .fig file delivered with the package/lab in question.

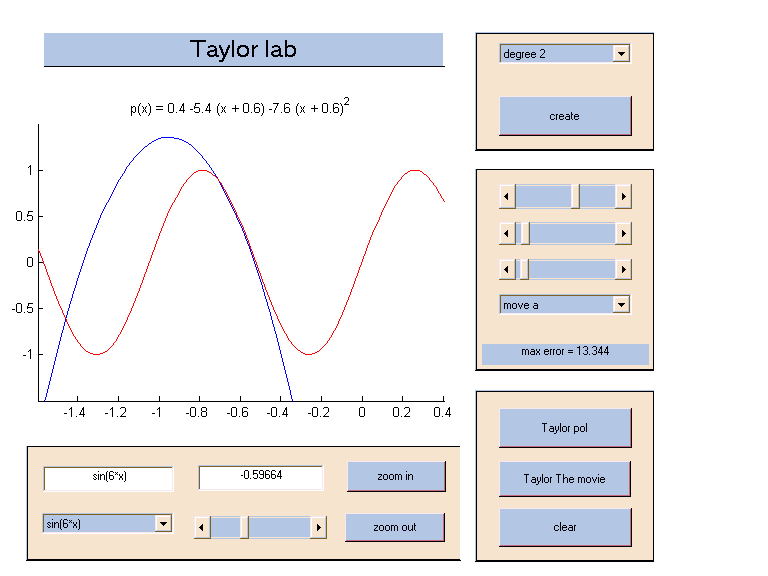
Polynomial approximation

To help the students understand polynomial approximation, we have developed a TaylorLab, for visualization of Taylor polynomials, and a PiecewisePolynomialLab for undestanding approximation by piecewise polynomial functions, used in modern computational methods for solving differential euqations.

Differential equations

Differential equations come in many different forms. A lab tool for better understanding so called two-point boundary value problems for second order such equations can be found in TwoPointBoundaryValueProblemsLab, and a tool that presents the finite element method in this context can be found in TPBVPFEMLab. These labs could be used as an introduction to computational mathematical modelling based on differential equations and the finite element method using piecewise polynomial approximation.

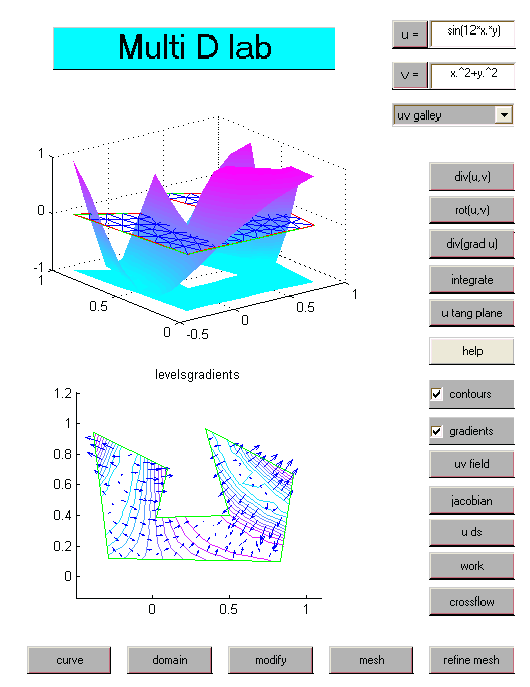
Multidimensional calculus and Finite element methods

To support important parts of a multi-dimensional calculus course, we have developed MultiDCalculusLab. In this you can learn about visualization of multidimensional fields using contour plots, vector plots, and graphs, get familiar with the basic differential operators grad, div, rot and div grad, and study the important integral theorems of Gauss, relating divergence to boundary outflow, and Stokes, relating interior rotation to a boundary work integral.

Once familiar with basic differential equation modelling in several dimensions, it is natural to get introduced to the finite element method in its simplest (multi-dimensional) form using the FiniteElementLab, and then the application labs PoissionsLab (for Poisson or Heat type equations) and NaviersLab (for Naviers equations in elasticity).

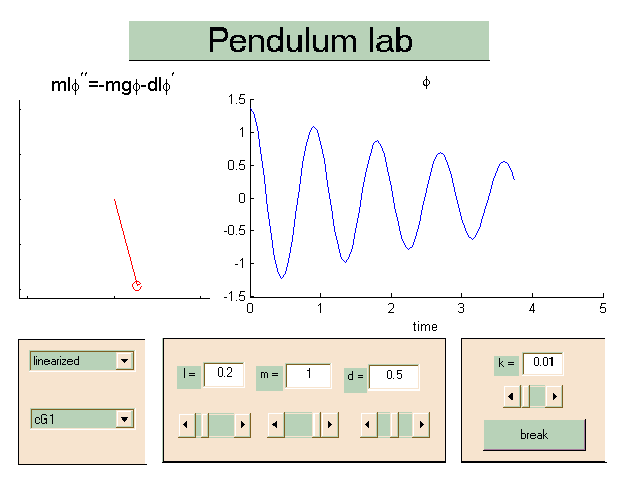
Applications

A few tools related to dynamical systems type applications can be found in PendulumLab, specifically illustrating the role of linearization, in the context of the pendulum equation, but also the role of the discretization method, where an important limitations of the classical explicit Euler method is demonstrated (adds artificial numerical energy) with the conservative cG1 or trapezoidal method as a contrast.



Another tool demonstrates how more complicated mechanical systems can be modelled and simulated using the same compuational technique in MiniMechLab.

A third example involving dynamical systems is the RoboticsLab. In this lab you can build a robot model, "joystick" the robot, and study also the inverse kinematics problem by specifying a target point for the robot to move to.

New tools for studying the simplest first and second order dynamical systems (ode's) is under development.

Algebra and geometry

On a more basic level, the VectorCalculatorLab lab, may be used to illustrate elementary vector algebra, matrix-vector multplication, orthogonal projection, the algebra for complex numbers etc, etc.

Similarly, EuclidLab is supposed to illustrate how a system of linear equations may be interpreted geometrically two ways, in the x-space or in the column-space, and also the concept of a over-determined such system and the least square approximate solution.

The Graph Gallery

The GraphGallery is thought of as a gallery with a "first floor" for graphs of simple one-variable functions, with rooms "exibiting" graphs of various types of such functions, like polynomials, exponentials, trigonometic functions etc, and a "second floor", with functions of several variables and vector valued functions.

A separate tool has been designed for mappings in terms of complex variables and can be found in ComplexLab.

Basics math

We have also developed tools for very basic math concepts such as SequencesLab, LipschitzLab, InverseFunctionLab, LinearizationLab, IntegrationLab.



Math Road map

Most of the demonstration and lab tools mentioned above can be accessed through a Road Map tools called MathRoadMap. What this interface does is simply to open a specific tool among the ones mentioned above.

Development

Many of the tools presented here are still under development, may not always function as desired. Please feel welcome to interact and participate in the further development by presenting constructive feedback whenever deeped appropriate. You are also welcome to suggest new tools covering new areas of math. For example, a tool illustrating partial derivatives and optimization is under construction, and another one illustrating forurier analysis is also to be added.

Platform independence

Most of the existing labs were developed on a unix platform while some may have been modified for a better look on a pc system. If you find some of these labs not so "good looking", you may interprete this as the lab being designed for another environment. Hopefully, a "next version" of these labs will be able to adapt to the platform on which they are run.

Example code and Code shells

To support our courses we have also produced a large number of .m files with example code for various purposes, and code shells which could consist of just a "header" for code specifying what the code (when written) should do, to code with some (key) parts missing for students to fix. Below you find a list of some of this code with a short specification of its purpose.

Disclaimer

ML comes with no guarantee to give correct solutions. In fact, there are known bugs and you can expect to find lots of "new" bugs in many of these lab tools. Occationally you may even find that matlab will "crash" as a result of trying to run some of these labs.