Problem 2 - Applications of solving linear systems

1. Linear Transformations

   The matrix 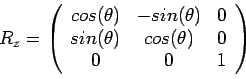$$R_z = \left( \begin{array}{ccc} cos(\theta) & -sin(\theta) & 0\\ sin(\theta) & cos(\theta) & 0\\ 0 & 0 & 1 \end{array}\right)$$ represents the rotation of the angle $\theta$ around the z-axis. $y = R_z x$ gives that y will be x rotated $\theta$ degrees around the z-axis.

   If you have time, visualize a rotation with the graphics system used in the A7 session. Draw both $x$ and $R_z x$ for some vectors $x$.

2. Inverting Linear Transformations

   The equation $R_z x = b$, where $R_z$ is the rotation matrix given above, $x$ is unknown and $b$ is a known vector, gives that x will be rotated by $R_z$ and produce $b$. But here we only have $b$, we don't have $x$. Here we need to solve the equation $R_z x = b$ to find $x$. Select a simple angle $\theta$ ( $\frac{pi}{2}$ for example) and solve $R_z x = b$ using Gaussian elimination, verify with Matlab.

   If you have time, visualize this new situation with the graphics system. Draw both x and b and verify visually that x is rotated back from b.

3. More Linear Transformations

   Do the same for other linear transformations from the AMBS book. Which ones are invertible and which ones aren't?