Problem

Solve the convection-diffusion equation on the unit square (square.m) with homogeneous Neumann boundary conditions, $a = 0.1$, $b = (-2,0)$, initial condition $u_0 = 0$, and $T = 3.5$, using a time step of size $k = 0.05$.

Let the source term (the right-hand side) be given by

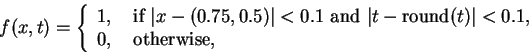$$f(x,t) = \left\{ \begin{array}{l} 1, \quad \mbox{if } \v... ...rt < 0.1, \\ 0, \quad \mbox{otherwise}, \end{array} \right.$$ (4)

corresponding to a new drop being added at $x = (0.75, 0.5)$ every second.

To solve the problem, look at your solver for the heat equation from computer session E2, or try yourself without looking.

Plot the solution using the pdesurf command in each time step. Remember to write pause after each plot.

Check your answer: Your solution should increase close to $x = (0.75, 0.5)$ every whole second (including $t = 0$). It should then drift off in the direction of the convection to the left, and be gradually flattened out by the diffusion, until a new drop is added at the next whole second.