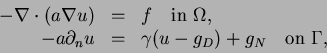Background

The variational formulation of Poisson's equation

$$\begin{array}{rcl} - \nabla \cdot (a \nabla u) &=& f \quad... ...=& \gamma (u - g_D) + g_N \quad \mbox{on } \Gamma, \end{array}$$ (1)

is given by

$$\int_{\Omega} a \nabla u \cdot \nabla v \, dx + \int_{\Gam... ... + \int_{\Gamma} (\gamma g_D - g_N) v \, ds \quad \forall v.$$ (2)

Using this general form, we can specify both Dirichlet boundary conditions (values of $u$ on the boundary) and Neumann boundary conditions (values of $\partial_n u)$ on the boundary).

Before today's computer session, make sure that you understand and can answer the following questions.

Question 1 Derive the variational formulation (2) from Poisson's equation (1).

Question 2 How do you specify Dirichlet and Neumann boundary conditions using the general boundary condition in (1)?

Question 3 Verify that $u(x) = \sin(\pi x_1) \sin(2\pi x_2)$ is a solution of Poisson's equation on the unit square $\Omega=(0,1)\times(0,1)$ with right-hand side $f(x) = 5 \pi^2 \sin(\pi x_1) \sin(\pi x_2)$. What are the boundary conditions?