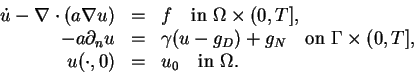Background

Today, we will solve the heat equation,

$$\begin{array}{rcl} \dot{u} - \nabla \cdot (a \nabla u) &=&... ..., \\ u(\cdot,0) &=& u_0 \quad \mbox{in } \Omega. \end{array}$$ (1)

The $\mathrm{dG}(0)$ formulation of the heat equation is given by

$$\begin{array}{ll} \int_{\Omega} U_n v \, dx + k \int_{\Om... ...{\Omega} U_{n-1} v \, dx \quad \forall v \in V_h, \end{array}$$ (2)

where $k = t_n - t_{n-1}$ denotes the size of the time step, $U_n$ denotes the value at $t=t_n$, and $U_{n-1}$ denotes the value at $t=t_{n-1}$. Note that also $\gamma$, $g_D$, and $g_N$ should be evaluated at $t=t_n$. The $\mathrm{dG}(0)$ method is also known as the backward Euler method.

Note that this computer session combines what you already know about time-stepping (from the C sessions), and what you know about solving stationary partial differential equations (from the D sessions and session E1).

Before today's computer session, make sure that you understand and can answer the following questions.

Question 1 Derive the variational formulation (2) from the heat equation (1).

Question 2 How does the corresponding variational formulation look for the $\mathrm{cG}(1)$ method? This method is also known as the Crank-Nicolson method.

Question 3 Verify that

$$u(x) = x_1 (1-x_1) x_2 (1-x_2) \sin t$$ (3)

is a solution of the heat equation on the unit square $\Omega=(0,1)\times(0,1)$ with $a=1$ and right-hand side

$$f(x,t) = x_1 (1-x_1) x_2 (1-x_2) \cos t + 2 ( x_1 (1-x_1) + x_2 (1-x_2) ) \sin t.$$ (4)

What are the boundary conditions?