


Next: Problem 2
Up: Problem 1
Previous: Preparation
Solve the heat equation on the unit square (square.m)
with homogeneous Dirichlet
boundary conditions, 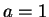 , initial condition
, initial condition 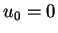 ,
, 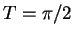 , and the right-hand side given by
, and the right-hand side given by
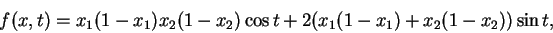 |
(5) |
using a time step of size 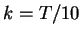 .
.
Compare your computed solution 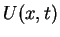 with the exact solution
with the exact solution 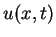 .
How large is the error in the maximum norm at the final time?
The maximum norm of the error is given by
.
How large is the error in the maximum norm at the final time?
The maximum norm of the error is given by
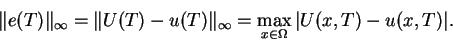 |
(6) |
How large is the error when you refine the mesh (square_refined.m)?
How large is the error when you divide the time step with a factor 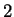 ?
?
To help you solve the problem, we will guide you through the implementation,
step by step. Don't look at these instructions if you want to solve the problem
in your own way. (You could of course glance occasionally at the instructions.)
- We start by implementing the time-stepping loop. Write a loop that takes
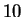 time steps and updates a variable called time, starting at time = 0.
Note that you should name the time variable time instead of t, since t
is used for the mesh.
time steps and updates a variable called time, starting at time = 0.
Note that you should name the time variable time instead of t, since t
is used for the mesh.
- Next, we add two vectors U0 and U1, representing the solution at time
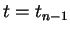 and time
and time 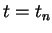 respectively. Initialize both vectors to zero (of the correct size), and
update the vector U0 to be equal to U1 at the beginning of every time step.
Remember to load the mesh at the beginning of the program.
respectively. Initialize both vectors to zero (of the correct size), and
update the vector U0 to be equal to U1 at the beginning of every time step.
Remember to load the mesh at the beginning of the program.
- We now need to assemble the matrix A for the left-hand side and the vector b
for the right-hand side of the variational formulation. The matrix is not time-dependent, so it
is enough if we assemble it one time, before the time-stepping begins. Since the vector depends on time
(
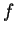 is time-dependent), we need to assemble it in each step of the loop.
is time-dependent), we need to assemble it in each step of the loop.
Note that the old value 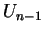 (given by U0) is present in the right-hand side of the variational formulation
(2). We thus need to supply this value to the assembler. This is done by using the extra argument
W of the program AssembleVector.m. In your program Heat.m, you then obtain the value of
(given by U0) is present in the right-hand side of the variational formulation
(2). We thus need to supply this value to the assembler. This is done by using the extra argument
W of the program AssembleVector.m. In your program Heat.m, you then obtain the value of
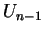 in the variable w.
in the variable w.
- Now solve the linear system to compute the new value of U1 in each step of the loop.
Compute the exact solution at final time and compute the error.
Check your answer: You should obtain the following errors in the maximum norm for the two different meshes
and the different values of 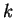 :
:
| |
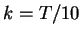 |
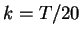 |
| grid.m |
0.000998 |
0.000876 |
| grid_refined.m |
0.000445 |
0.000318 |



Next: Problem 2
Up: Problem 1
Previous: Preparation
Christoffer Cromvik
2004-04-25
![]() , initial condition
, initial condition ![]() ,
, ![]() , and the right-hand side given by
, and the right-hand side given by
![]() with the exact solution
with the exact solution ![]() .
How large is the error in the maximum norm at the final time?
The maximum norm of the error is given by
.
How large is the error in the maximum norm at the final time?
The maximum norm of the error is given by
![]() (given by U0) is present in the right-hand side of the variational formulation
(2). We thus need to supply this value to the assembler. This is done by using the extra argument
W of the program AssembleVector.m. In your program Heat.m, you then obtain the value of
(given by U0) is present in the right-hand side of the variational formulation
(2). We thus need to supply this value to the assembler. This is done by using the extra argument
W of the program AssembleVector.m. In your program Heat.m, you then obtain the value of
![]() in the variable w.
in the variable w.
![]() :
: