


Next: Preparations
Up: Convection-diffusion
Previous: Convection-diffusion
Today, we will solve the time-dependent convection-diffusion equation,
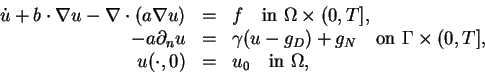 |
(1) |
where the convection is given by the vector 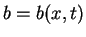 and the
diffusion is given by
and the
diffusion is given by 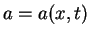 .
The
.
The
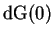 formulation of the convection-diffusion equation is given by
formulation of the convection-diffusion equation is given by
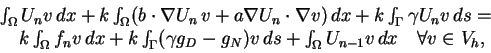 |
(2) |
where
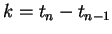 denotes the size of the time step,
denotes the size of the time step, 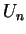 denotes the value at
denotes the value at 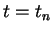 ,
and
,
and 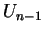 denotes the value at
denotes the value at 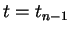 . Note that also
. Note that also 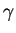 ,
, 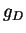 , and
, and 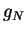 should
be evaluated at
should
be evaluated at 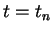 . The
. The
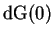 method is also known as the backward Euler method.
method is also known as the backward Euler method.
Before today's computer session, make sure that you understand and can
answer the following questions.
Question 1
Derive the variational formulation (2) from
the convection-diffusion equation (1).
Question 2
How does the corresponding variational formulation look for the
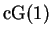 method?
This method is also known as the Crank-Nicolson method.
method?
This method is also known as the Crank-Nicolson method.
Question 3
Verify that
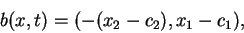 |
(3) |
where 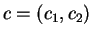 is a constant, is divergence-free, i.e.,
is a constant, is divergence-free, i.e.,
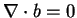 . Draw a simple sketch of the
vector-field given by
. Draw a simple sketch of the
vector-field given by 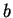 . (Draw some arrows on a piece of paper.) Why is it important
that
. (Draw some arrows on a piece of paper.) Why is it important
that 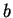 is divergence-free?
is divergence-free?



Next: Preparations
Up: Convection-diffusion
Previous: Convection-diffusion
Christoffer Cromvik
2004-04-25
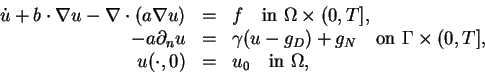
![]() method?
This method is also known as the Crank-Nicolson method.
method?
This method is also known as the Crank-Nicolson method.