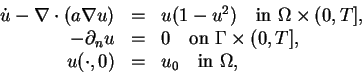Background

Today, we will solve the bistable equation,

$$\begin{array}{rcl} \dot{u} - \nabla \cdot (a \nabla u) &=&... ..., \\ u(\cdot,0) &=& u_0 \quad \mbox{in } \Omega, \end{array}$$ (1)

where we note that the right-hand side depends on the solution $u$ itself. This is a nonlinear equation (including terms with both $u^2$ and $u^3$). We call this a reaction-diffusion equation, since it contains both the diffusive term $- \nabla \cdot (a \nabla u)$ and a term depending only on $u$, the reaction term $u(1-u^2)$.

The $\mathrm{dG}(0)$ formulation of the bistable equation is given by

$$\begin{array}{ll} \int_{\Omega} U_n v \, dx + k \int_{\Om... ...{\Omega} U_{n-1} v \, dx \quad \forall v \in V_h, \end{array}$$ (2)

where $k = t_n - t_{n-1}$ denotes the size of the time step, $U_n$ denotes the value at $t=t_n$, and $U_{n-1}$ denotes the value at $t=t_{n-1}$.

Before today's computer session, make sure that you understand and can answer the following questions.

Question 1 Derive the variational formulation (2) from the bistable equation (1).

Question 2 How does the corresponding variational formulation look for the $\mathrm{cG}(1)$ method? This method is also known as the Crank-Nicolson method.

Question 3 Try to find three stationary solutions of the bistable equation. Hint: For which values of $u$ is the right-hand side zero? Which of these stationary solutions are stable, i.e., if we perturb the stationary solution slightly, will it then try to go back to the stationary state or will it continue to change? Why do you think the equation is called the bistable equation?